数理方法-弦振动方程与热传导方程

弦振动方程

方程

二维

{u_{tt}} - {a^2}{u_{xx}} = f(t,x),t > 0,x \in R

高维

{u_{tt}} - {a^2}\Delta u = f(t,x),t > 0,x \in R

边界条件

Dirichlet边界条件

u(t,a) = \varphi (t),\forall t>0，表示弦的端点x=a的位移随时间t的变化是预先给定的

Neumaan边界条件

\frac{{\partial u}}{{\partial x}}(t,a) = \mu (t)，表明振动的力是预先给定的

Robin边界条件

{\left. {\left( {\frac{{\partial u}}{{\partial x}} - \sigma u} \right)} \right|_{x = a}} = 0，表明a端与线性弹簧相连。如果弹簧是非线性，则\sigma \to \sigma (u)

热传导方程

方程

{u_t} - {a^2}\Delta u = f(t,M)

边界条件

Dirichlet边界条件

{\left. u \right|_s} = {\mu _1}，表面温度已知

Neumaan边界条件

\frac{{\partial u}}{{\partial \overrightarrow n }} = {\mu _2}，表面热流已知

Robin边界条件

{\left. {\left( {\frac{{\partial u}}{{\partial \overrightarrow n }} + \sigma u} \right)} \right|_s} = {\mu _3}，导体被放在温度为\mu_3的环境中

两种方程的推导

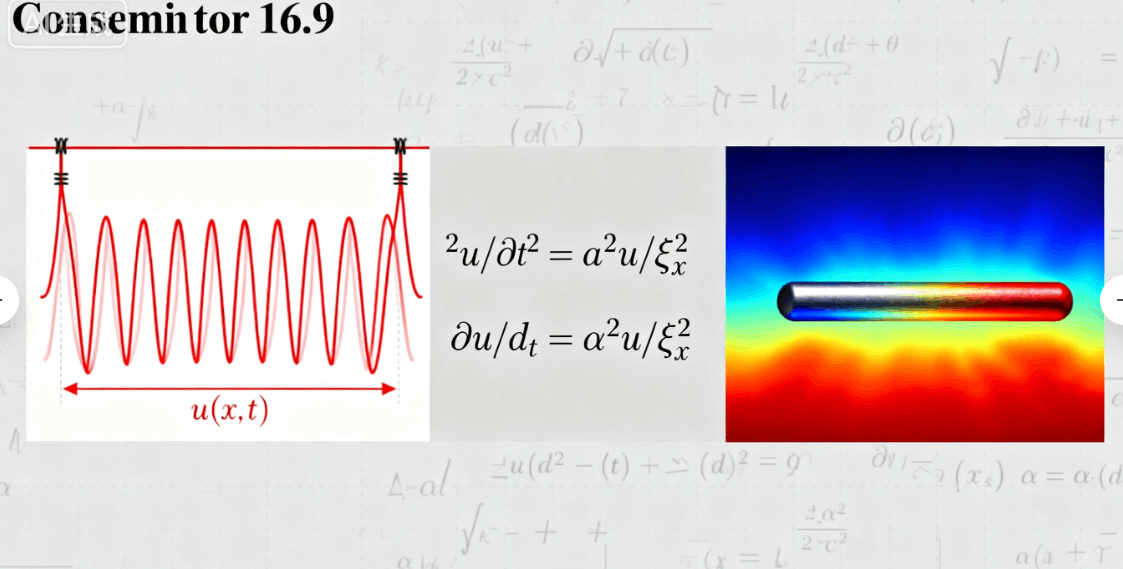
弦振动方程

u(x,t) 中的 x 代表原本位于弦上 x 处的点，在 t 时刻位于 u 处

热传导方程